Nota: Esta entrada realiza los test en Python pero el concepto aplica a otros lenguajes.
Desde nuestra educación escolar nos enseñan que 1 + 1 = 2 es un hecho lógico y cierto, avanzando en los conocimientos aprendemos a sumar, restar, dividir y multiplicar no solo números sino fracciones, por ende 1/10 + 1/10 + 1/10 = 3/10 o puesto de otra manera 0.1 + 0.1 + 0.1 = 0.3. Con estas ideas en mente pensamos que nuestras calculadoras y computadoras trabajan de la misma manera.
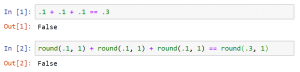
Ponga mucha atención a esta imagen de un Jupyter Notebook en Python
¿Por qué ocurre esto en Python?
Si ponemos atención a la primera entrada del notebook la ecuación da como resultado falso. ¿Por qué? Al trabajar con números decimales nos acercamos a los límites de la representación numérica que puede hacer un computador. Esto se debe a que el número decimal “0.1” no es un valor representable en base binaria, que es la forma en que el procesador suma y resta los números. Para poder trabajar con este valor el computador busca la representación más cercana al valor decimal utilizando base binaria, obteniendo un valor periódico binario:
0.0001100110011001100110011001100110011001100110011…
Al frenar en cualquier número finito de bits se obtendrá una aproximación. En la mayoría de las máquinas actuales, los decimales/float se aproximan usando una fracción binaria con un numerador de 53 bits y el denominador como una potencia de dos. En el caso de 1/10, la fracción binaria es:
3602879701896397/(2^55)
La mayoría de los usuarios no son conscientes de esta aproximación por la forma en que se muestran los valores en la pantalla. En este caso, Python solamente muestra una aproximación respecto al valor verdadero almacenado por la máquina. En la mayoría de las máquinas, si Python fuera a imprimir el verdadero valor decimal de la aproximación binaria almacenada para 0.1, debería mostrar esto:
0.1000000000000000055511151231257827021181583404541015625
A partir de la posición 18 aparecen valores que el usuario no ve directamente al escribir código pero que están ahí al realizar la operación de suma, por este motivo la primera igualdad del nootbook da falso.
Esto no es un problema único de Python, sino una realidad en varios lenguajes de programación que implementan el estándar de aritmética de punto flotante IEEE-754 como Perl, C, C++, Java, Fortran, entre otros.
¿Cómo solucionamos esto?
Para solucionar los riesgos de precisión se puede utilizar herramientas que permitan un redondeo adecuado de los valores representativos. Para el ejemplo planteado podemos redondear hasta 16 dígitos si ser afectados por los decimales residuales.
Recomendamos utilizar los módulos decimal y fractions de Python para representar valores decimales. Esto facilitara operaciones aritméticas y el intercambio de información con otros sistemas sin perder exactitud.
Si te gusta programar en Python puede que estas entradas (MakeHealthChile parte 1 y MakeHealthChile parte 2) relacionadas te sirvan de inspiración, ir al final de cada una.
Nota: Si crees que este contenido puede ser útil para otras personas no dudes en compartirlo. De igual forma te invitamos a seguirnos en Linkedin, Facebook y Youtube donde estamos publicando semanalmente tips relacionados con Business Intelligence & Data Warehouse, Data Science, Visualización de Datos y Software a la Medida.